延迟线位置偏差对太赫兹时域光谱系统的测量不确定度影响分析董海龙, 汪家春^*, 赵大鹏, 陈宗胜, 刘瑞煌, 时家明 摘要

太赫兹时域光谱技术可以快速准确地提取材料在太赫兹波段的光学常数。 然而, 其各组成部分在控制精度、 响应误差、 系统噪音以及实验操作、 数据处理等方面的误差, 将影响系统对材料光学常数提取的准确性。 基于透射式太赫兹时域光谱系统的测量原理, 分析了系统延迟线位置偏差对提取材料复折射率准确度的影响, 建立了误差在样品测量过程中的传递模型, 并利用MATLAB仿真了误差对提取样品复折射率影响。 结果表明, 样品折射率和消光系数的不确定度受到了系统延迟线位置偏差的影响, 且系统延迟线位置偏差越大, 样品的复折射率提取的不确定度也就越大。 同时, 相比消光系数, 延迟线位置的偏差对样品折射率的不确定度具有更大的影响。 该模型具有一定的实际意义和理论参考价值, 可分析系统延迟线位置偏差对太赫兹时域光谱系统提取材料光学常数不确定度的影响, 为优化太赫兹时域光谱系统提供理论指导。

关键词: 太赫兹时域光谱系统; 复折射率; 延迟线位置偏差; 测量不确定度中图分类号:O433.4 文献标志码:AAnalysis of Measurement Uncertainty in THz-TDS Carried by Delay-Line Position DeviationDONG Hai-long, WANG Jia-chun^*, ZHAO Da-peng, CHEN Zong-sheng, LIU Rui-huang, SHI Jia-ming AbstractKeyword: THz-TDS; Complex index of refraction; Delay-line position deviation; Measurement uncertainty文章图片引 言

太赫兹时域光谱(Teraherz time domain spectroscopy, THz-TDS)技术是20世纪末发展起来的光谱技术。 图1是透射式THz-TDS的结构图, 其光谱分析属于相干分析, 来自相同激光光源的一束激光经分束镜后, 一束进入发射天线产生太赫兹波, 透过样品。 另一束激光经过延迟装置进入探测天线, 对经过样品的太赫兹波进行数值采样, 得到时域光谱。 对时域信号进行离散傅里叶变换, 得到频域光谱。

	Figure Option
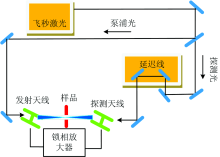	图1 透射式THz-TDS结构图Fig.1 Assumption diagram of transmitted THz-TDS

基于相干辐射的特点, THz-TDS可以有效地测量材料在太赫兹波段的振幅和相位, 得到太赫兹波段的物理和化学信息, 用于提取材料在太赫兹波段的光学常数^[1, 2], 如复折射率、 介质损耗、 电导率、 吸收系数等, 在半导体材料^[3]、 电介质材料^[4]以及超材料^[5]等研究中具有重要作用。

常用的THz-TDS主要有透射式、 反射式THz-TDS, 而透射式THz-TDS是目前最成熟、 应用最广泛的系统, 广泛用于提取非极性物质、 非金属物质太赫兹波段的光学常数^[6, 7, 8]。 而THz-TDS通常由机械装置、 光学部件和电子元件等部分组成, 各个部分的控制精度、 响应误差、 系统噪声以及实验操作、 数据处理等方面均会影响材料光学常数的准确性, 分析THz-TDS测试的不确定度对于准确提取材料光学常数具有至关重要的意义^[9, 10]。 因此, 本文将基于透射式THz-TDS测量原理, 从延迟线位置偏差方面分析其对材料光学常数准确度的影响, 研究系统延迟线误差对提取材料光学常数不确定度的影响程度。

1 透射式THz-TDS提取材料光学常数原理

材料的光学常数不是常数, 而是频率的函数。 这些参数之间是相互关联的, 一般可利用已知的一个或者一组参数可以计算出其他参数。 通常, 我们用材料的复折射率描述其宏观光学性质, 可表示为 n~�~(w)=n(w)-jk(w), 其中, w为角频率, n(w)为材料的折射率, 描述材料的色散情况; k(w)为材料的消光系数, 描述材料的损耗。

材料复折射率 n~�~(w)和复介电常数 ε~�~(w)之间存在平方关系, 通过 n~�~(w)可获得 ε~�~(w), 即 ε~�~(w)=( n~�~(w))²=(n(w)-jk(w))²。 材料吸收系数α (w)也可以通过消光系数求得。

基于菲涅尔公式, Dorney等提出了利用THz-TDS测量样品光学常数的模型^[8]。 该模型在分析和测量样品光学常数的过程中, 忽略样品表面粗糙度对太赫兹波的散射作用, 即认为所测样品的表面保持光滑和相对平行。

如图2, 入射太赫兹脉冲由介质a进入介质b, 并在其间发生透射和反射, 由介质b射出介质a。 根据文献分析, 可以得到样品的复透过率(包括振幅透过率和相位延迟) H~�~(w)

H~(w)=ETHz(w)Eref(w)=4n~air(w)n~sam(w)cosθcosβ[n~air(w)cosβ+n~sam(w)cosθ]2×(exp{−j[ln~sam(w)−ΔLn~air(w)]wc})FP(w)(1)�~(�)=�THz(�)�ref(�)=4�~air(�)�~sam(�)cos�cos�[�~air(�)cos�+�~sam(�)cos�]2×exp-�[��~sam(�)-Δ��~air(�)]��FP(�)(1)

	Figure Option
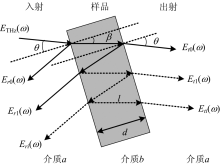	图2 太赫兹波在样品中的透射与反射Fig.2 Transmission and reflection of THz wave in the sample

式(1)中, θ 和β 分别为太赫兹脉冲的入射角和折射角, n~air�~air(w)和 n~sam�~sam(w)分别为介质a和介质b的复折射率, d为样品厚度, l为太赫兹脉冲在样品中传输距离, Δ L为光程差, FP(w)是太赫兹脉冲在样品内部多次反射, 产生Fabry-Perot标准具效应所引起的结果, FP(w)= ∑k=0m∑�=0�[ r2kbap2ksam�ba2��sam2�(w, l)]。 在实际操作中, 通常让太赫兹脉冲垂直入射到被测样品表面上。 此时, θ =β =0, Δ L=l=d, 并认为空气折射率 n~air�~air(w)=1。 当样品较厚的情况, 反射波的光程较大, 此时不考虑所有回波, 忽略多次反射, 即此时m=0, FP(w)=1, 则复透过率 H~�~(w)简化为

H~(w)=ETHz(w)Eref(w)=4n~sam(w)[1+n~sam(w)]2×exp{−jwl[n~sam(w)−1]c}(2)�~(�)=�THz(�)�ref(�)=4�~sam(�)[1+�~sam(�)]2×exp-�wl[�~sam(�)-1]�(2)

复透过率 H~�~(w)又可写成模和幅角的形式, 即 H~�~(w)= |H(w)|�(�)exp[-jφ _c(w)], 可以得到样品的折射率和消光系数

n(w)=cwdφc(w)+1(3)k(w)=cwdln{4n(w)|H(w)|[n(w)+1]}(4)�(�)=�wd��(�)+1(3)�(�)=�wdln4�(�)�(�)[�(�)+1](4)

由式(3)可知, 利用方差计算, 获得样品折射率的方差为

σ2n(w)=[cwd2φc(w)]2σ2d+[cwd]2σ2φc(w)(5)��2(�)=���2��(�)2��2+�wd2���2(�)(5)

由式(5), 样品的折射率不确定度是由样品厚度误差 σ2d��2, 系统引起的相位误差产生 σ2φc���2(w)。 由式(4)可得样品消光系数的方差为

σ2k(w)=[k(w)d]2σ2d+[cwd|H(w)|]2σ2|H|(w)+[cwd(n(w)−1n(w)+1)]2[σ2n(w)n(w)2+1](6)��2(�)=�(�)�2��2+�wd�(�)2�|�|2(�)+�wd�(�)-1�(�)+12��2(�)�(�)2+1(6)

2 延迟线位置偏差与THz-TDS测量不确定度的关系

在THz-TDS中, 通过两块相互垂直的反射镜的机械移动实现对探测光脉冲的光程调节, 延迟线位置的准确性会直接影响波门探测的采样时间, 从而导致探测到的太赫兹脉冲信号的振幅存在误差。 图3为延迟线位置与采样得到的时域信号。 当延迟线位于x_k位置时, 如果其偏移Δ x, 则探测系统的采样时间, 即时间延迟将偏移Δ t, Δ t= 2Δxc2Δ��, 由此可得到时间延迟的方差 σ2t��2= 4σ2xc24��2�2, σ2x��2为延迟线位置的方差。

	Figure Option
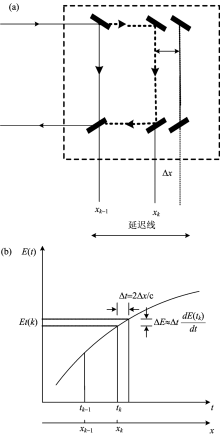	图3 延迟线与时域信号Fig.3 Delay line and time domain signal

由图3可以看出, 由于延迟线位置的偏移引起的时域信号振幅的测试误差为Δ E, 忽略其他噪声的影响, 采样获得的时域信号的振幅值应等于t_k时刻幅值的准确值E(t_k)与误差Δ E之和, 即E(k)=E(t_k)+Δ E=E(t_k)+Δ t dE(tk)dtd�(��)d�, t_k=kτ , τ 为采样间隔。 测试信号的振幅的方差可表示为 σ2E��2(k)= σ2E��2(t_k)+ σ2t[∂E(tk)∂t]2��2∂�(��)∂�2, 振幅方差 σ2E��2(t_k)是由系统噪声引起的, σ2t[∂E(tk)∂t]2��2∂�(��)∂�2是延迟线位置偏差引起的误差。 忽略噪声误差, 可得延迟线位置的偏差引起的误差为 σ2E��2(k)= [2c∂E(kτ)τ∂k]2σ2x2�∂�(kτ)�∂�2��2。

对于采样得到的信号进行离散傅里叶变换, 可得

E(ω)=Er(ω)+jEi(ω)=∑k=0N−1E(k)exp(−jωkτ)(7)E(ω)=��(ω)+j��(ω)=∑�=0�-1�(�)exp(-jωkτ)(7)

由式(7)可得频域信号的实部和虚部分别如式(8a)和式(8b)

Er(ω)=∑k=0N−1E(k)cos(ωkτ)(8a)Ei(ω)=−∑k=0N−1E(k)sin(ωkτ)(8b)��(ω)=∑�=0�-1�(�)cos(ωkτ)(8a)��(�)=-∑�=0�-1�(�)sin(ωkτ)(8b)

假定各个采样时刻的振幅值均相互独立, 则实部和虚部的方差以及两者的协方差分别为

σ2Er(ω)=∑k=0N−1cos2(ωkτ)σ2E(k)(9a)σ2Ei(ω)=∑k=0N−1sin2(ωkτ)σ2E(k)(9b)σ2ErEi(ω)=−∑k=0N−1sin(ωkτ)cos(ωkτ)σ2E(k)=−12∑k=0N−1sin(2ωkτ)σ2E(k)(9c)���2(�)=∑�=0�-1cos2(ωkτ)��2(�)(9a)���2(�)=∑�=0�-1sin2(ωkτ)��2(�)(9�)�����2(�)=-∑�=0�-1sin(ωkτ)cos(ωkτ)��2(�)=-12∑�=0�-1sin(2ωkτ)��2(�)(9c)

信号的振幅和相位可由复振幅的实部和虚部确定, 即

|E(ω)|=Er(ω)2+Ei(ω)2−−−−−−−−−−−−−√(10a)∠E(ω)=arctanEi(ω)Er(ω)(10b)�(�)=��(�)2+��(�)2(10a)∠�(�)=arctan��(�)��(�)(10b)

相应的振幅和相位的方差分别为

σ2|E|�|�|2(ω )= 1|E(ω)|21�(�)2[E_r(ω )² σ2Er���2(ω )+E_i(ω )² σ2Ei���2(ω )+2E_r(ω )E_i(ω ) σ2ErEi�����2(ω )](11a)

σ2∠E�∠�2(ω )= 1|E(ω)|41�(�)4[E_i(ω )² σ2Er���2(ω )+E_r(ω )² σ2Ei���2(ω )-2E_r(ω )E_i(ω ) σ2ErEi�����2(ω )](11b)

将式(9a), 式(9b)和式(9c)带入式(11a)可得相应的振幅方差为

σ2|E|(ω)=1|E(ω)|2∑k=0N−1[Er(ω)cos(ωkτ)−Ei(ω)sin(ωkτ)]2σ2E(k)(12a)�|�|2(�)=1�(�)2∑�=0�-1[��(�)cos(ωkτ)-��(�)sin(ωkτ)]2��2(�)(12a)

将样品信号和参考信号分别代入式(12a), 可得样品信号和参考信号振幅的方差。

将式(9a), 式(9b)和式(9c)带入式(11b)可得相应的相位方差为

σ2∠E(ω)=1|E(ω)|4∑k=0N−1[Ei(ω)cos(ωkτ)+Er(ω)sin(ωkτ)]2σ2E(k)(12b)�∠�2(�)=1�(�)4∑�=0�-1[��(�)cos(ωkτ)+��(�)sin(ωkτ)]2��2(�)(12b)

将样品信号和参考信号分别代入式(12b), 可得样品信号和参考信号相位的方差。

在时域上, 系统的转移函数是通过对样品信号和参考信号进行反卷积运算获得, 同理, 在频域上, 通过两信号的振幅比和相位差即可获得转移函数的振幅和相位。 对于THz-TDS, 系统的转移函数即为复透过率 H~�~(w), 其振幅和相位可分别表示为

|H(ω)|=|Esam(ω)||Eref(ω)|(13a)∠H(ω)=∠Esam(ω)−∠Eref(ω)(13b)�(�)=�sam(�)�ref(�)(13a)∠�(�)=∠�sam(�)-∠�ref(�)(13b)

转移函数 H~�~(w)对应的振幅方差为

σ2|H|(ω)=1|Eref(ω)|2σ2|Esam|(ω)+|Esam(ω)|2|Eref(ω)|4σ2|Eref|(ω)(14a)σ2∠H(ω)=σ2∠Esam(ω)+σ2∠Eref(ω)(14b)�|�|2(�)=1�ref(�)2�|�sam|2(�)+�sam(�)2�ref(�)4�|�ref|2(�)(14a)�∠�2(�)=�∠�sam2(�)+�∠�ref2(�)(14b)

将式(12a)以样品信号和参考信号的数据代入式(14a), 可得系统转移函数的振幅方差为

σ2|H|�|�|2(w)= 1|Eref(w)|2|Esam(w)|2∑k=0N−11�ref(�)2�sam(�)2∑�=0�-1E_sam, r(w)cos(wkτ )-

E_sam, i(w)sin(wkτ )]² σ2Esam(k)��sam(�)2+

|Esam(w)|2|Eref(w)|6∑k=0N−1�sam(�)2�ref(�)6∑�=0�-1[E_ref, r(w)cos(wkτ )-

E_ref, i(w)sin(wkτ )]² σ2Eref(k)��ref(�)2(15a)

将式(12b)以样品信号和参考信号的数据代入式(14b), 可得系统转移函数的相位方差为

σ2∠H�∠�2(w)= 1|Esam(w)|4∑k=0N−11�sam(�)4∑�=0�-1[E_sam, i(w)cos(wkτ )+

E_sam, r(w)sin(wkτ )]² σ2Esam��sam2(k)+

1|Eref(w)|4∑k=0N−11�ref(�)4∑�=0�-1[E_ref, i(w)cos(wkτ )+

E_ref, r(w)sin(wkτ )]² σ2Eref��ref2(k)(15b)

在反卷积运算之后, 对转移函数进行相位展开即

ϕ(w)=∠H(w)+2πM(w)(16)�(�)=∠�(�)+2π�(�)(16)

式(16)中, M为一个整数, 由低频相位确定。 根据反正切函数的性质, 干涉相位的相位值被限制在[0, 2π ]之间, 即相位展开后的相位值是在限定范围内呈阶跃的不连续分布^[11]。 相位展开的目的是要使多个截断相位的区域拼接展开成连续相位, 故利用2π 的整数倍作为补偿相位值, 用来反映信号真实的相位变化。 相位的方差为

σ2ϕ(w)=σ2∠H(w)(17)��2(�)=�∠�2(�)(17)

然而, 由于低频部分的信噪比较低, 在相位展开过程中, 易引入噪声, 为减少噪声对相位的影响, 采用线性外推方法对相位进行修正。 对于式(16), 增加一个由最小二乘法拟合得到的偏移值b, 从而得到修正后的相位为

ϕc(w)=ϕ(w)+b(18)��(�)=�(�)+�(18)

式(18)中, b=f(ϕ ₁, ϕ ₂, …, ϕ _m)= ∑ϕi∑w2i−∑wi∑wiϕim(∑w2i−(∑wi)2/m)∑��∑��2-∑��∑�����(∑��2-(∑��)2/�), m为高信噪比范围内的采样点个数。

由式(18)可得修正后的相位的方差为

σ2ϕc(w)=σ2ϕ(w)+σ2b(w)+2σ2ϕb(w)(19)���2(�)=��2(�)+��2(�)+2�ϕb2(�)(19)

由式(5), 式(6)和式(19)可得延迟线位置偏差导致样品折射率和消光系数的误差为

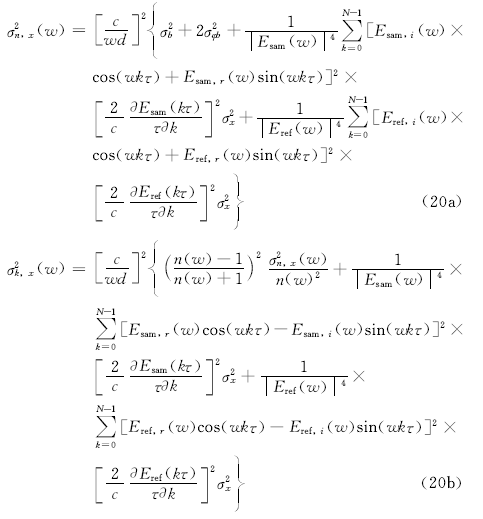
3 延迟线位置偏差对THz-TDS测量不确定度影响的仿真计算及结果分析3.1 透射式THz-TDS测量样品模型建立

根据Duvillaret等建立的光电导天线分析模型, 图4展示了太赫兹辐射经过空气和样品产生的太赫兹参考信号和样品信号^[12], 经过傅里叶变换得到参考信号和样品信号的频域信号。 样品选取复折射率 n~�~(w)=1.5-0.1j, 样品厚度l=1 mm, 空气折射率n₀=1, 入射角θ =0° 。

	Figure Option
	图4 太赫兹时域及频域信号Fig.4 Terahertz time domain and frequency domain signal

根据对透射式THz-TDS中采样信号分析及延迟线位置偏差对不确定度影响的分析, 以德国设计生产的TDS1010系统为参考, 取脉冲宽度为0.1 ps, 由Δ t= 2Δxc2Δ��可知, 延迟线位置变化X=15 μ m。 由式(20a)和式(20b), 取延迟线位置偏差的标准差σ _x=10 μ m, 研究不同频率下由σ _x导致提取样品折射率和消光系数的影响, 结果如图5所示。

	Figure Option
	图5 延迟线位置偏差σ x=10 μ m对光学常数标准差的影响 (a): 折射率的标准差; (b): 消光系数的标准差Fig.5 Standard deviation of optical constants affected by σ x=10 μ m (a): Standard deviation ofrefractive index; (b): Standard deviation of coefficient of light extinction

由图5可知, 样品光学常数的不确定度受系统延迟线位置偏差的影响, 在峰值频率处, 具有最小的标准差。 对比图5(a)和(b)两图可以发现, 相比消光系数, 延迟线位置的偏差对样品折射率的不确定度具有更大的影响。

取频率为1 THz, σ _x从10~20 μ m递增, 研究不同延迟线位置偏差的标准差对提取样品折射率和消光系数的影响, 结果如图6所示。

	Figure Option
	图6 1 THz下不同延迟线位置偏差对光学常数标准差的影响 (a): 折射率的标准差; (b): 消光系数的标准差Fig.6 Standard deviation of optical constants affected by different σ x in 1 THz (a): Standard deviation of refractive index; (b): Standard deviation of coefficient of light extinction

由图6可知, 在太赫兹脉冲频率一定的条件下, 透射式THz-TDS提取样品参数的不确定度受系统延迟线位置偏差的影响, 且延迟线位置偏差越大, 系统不确定度越大, 两者呈线性递增的关系。

根据以上对透射式THz-TDS延迟线位置偏差对不确定度影响的分析, 作延迟线位置偏差σ _x从10~20 μ m递增, 递增间隔为1 μ m, 不同频率下由σ _x导致提取样品折射率和消光系数的影响, 结果如图7所示。

	Figure Option
	图7 不同延迟线位置偏差对光学常数标准差的影响 (a): 折射率的标准差; (b): 消光系数的标准差Fig.7 Standard deviation of optical constants affected by σ x from 10 to 20 μ m (a): Standard deviation of refractive index; (b): Standard deviation of coefficient of light extinction

4 结 论

利用Dorney等提出的THz-TDS测量样品光学常数的模型, 分析了透射式THz-TDS延迟线位置偏差对提取样品复折射率不确定度的影响, 建立了误差在样品测量过程中的传递模型, 并利用MATLAB仿真了误差对提取样品复折射率不确定度的影响。 仿真结果表明, 样品折射率和消光系数的不确定度受系统延迟线位置偏差的影响, 系统延迟线位置偏差越大, 对样品的光学常数提取具有更大的不确定度。 在系统测量峰值频率处, 折射率和消光系数具有最小的标准差。 相比消光系数, 延迟线位置的偏差对提取样品折射率的不确定度具有更大的影响。 该模型可分析系统延迟线位置偏差对THz-TDS提取材料光学常数不确定度的影响程度, 为THz-TDS优化提供理论指导。

The authors have declared that no competing interests exist.

参考文献文献列表